「地球温暖化の影響で豪雨の頻度が2倍になる」といった報道がよくなされる。このようなコミュニケーションの在り方は適切かどうか、考察する。
・・・・・・・・・・・・・
定理
ある期間の積算降水量x mmの雨が極値統計理論に基づいて確率密度関数 f(x)に従っており、気温上昇によってこれがg(x)に変化する、と考える。
このとき、クラウジウス・クラペイロン効果(CC効果)による1℃の気温上昇に対する降水量の増加割合を+7%とすれば、確率密度関数はg(x)=f(x/1.07)となる。
さて
「x mm以上の雨の頻度が y 倍になる」
と言いたい場合、
任意のyに対して、かならずあるxが存在する。
・・・・・・・・・・・・・
一般的な証明は難しいので別の機会に譲り、以下、一つの事例で検証する。
検証
例として、1893–2020年の彦根地方気象台で観測された年最大日降水量データを用いると、再現期間T年の年最大日降水量x mm以上の降水事象が1年間に起きる確率(超過確率F)は、近似的に次の極値分布で表せる:
F(x)=1/T, (1)
T=0.18 exp (0.03 x), (2)
ここで、再現期間とはこれまでに経験した現象やそれらを超える規模の現象の発生頻度を表し、0.18と0.03は目視によるフィッティングで得た。(なお、明治時代に起きた「彦根豪雨」の596.9 mmは異常値としてここでは除外した。)
(1)式を用いると、元のデータとCC効果(+7%/+1℃)を考慮したデータの年最大日降水量に対する超過確率は下図のようになる。両者の比は出現頻度の倍率を表し、年最大日降水量50 mmを境に上昇を続けていくことがわかる(図中青線)。
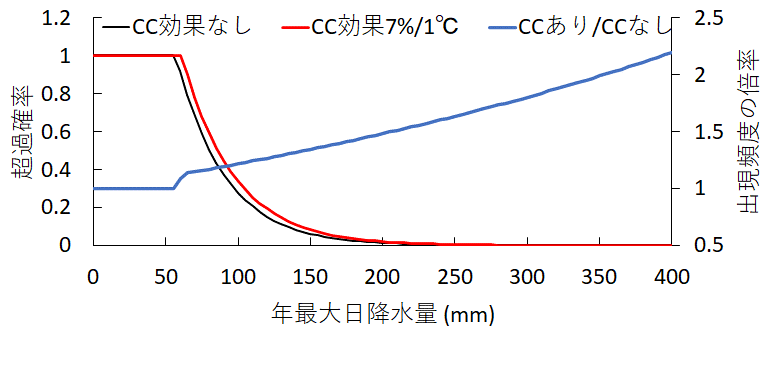
この計算例では、「1.5倍」になるのは約200mmを超える雨、「2倍」になるのは約350mmを超える雨、ということになる。
このように「y mm以上」という閾値によって「x倍」の倍数は大きく変わってしまう。
このようにしてみると、「豪雨がx倍の頻度になる」という表現の仕方は、「y mm以上」のということとセットで言わないと無意味だということが分かる。
従って、誤解の無いコミュニケーションの仕方としては、「豪雨の頻度が何倍になる」と言うのではなく、もしも雨量が7%増えるということであれば、そのまま単に「雨量が7%増える」と言うのに留めておいた方がよい。
それに、どのような対応を採ればよいのか、と言う防災の観点にも直結する。もしも雨量が7%増えるのであれば、防災のための計画雨量(対象雨量とも呼ぶ)を7%増やし、あとは通常の防災投資をすればよい。つまり、計画雨量に対応してダムの貯水量や河川の流量を設計し、堤防を建設したり河床の堆積物をさらったりすればよい。
謝辞
彦根地方気象台の年最大日降水量データは、気象庁ホームページから取得した。
参考文献
堅田元喜、極値統計学の考え方 ―異常気象は、それほど異常ではない?―
https://cigs.canon/article/20210524_5806.html
堅田元喜、地球温暖化によって、日本の大雨は何割増えたのか?
https://ieei.or.jp/2022/04/expl220428/
杉山大志 【研究ノート】豪雨の原因は地球温暖化か?
https://cigs.canon/uploads/2020/07/20200730_sugiyama_report.pdf
国土交通省 河川砂防技術基準 調査編
https://www.mlit.go.jp/river/shishin_guideline/gijutsu/gijutsukijunn/chousa/pdf/chousa_all.pdf
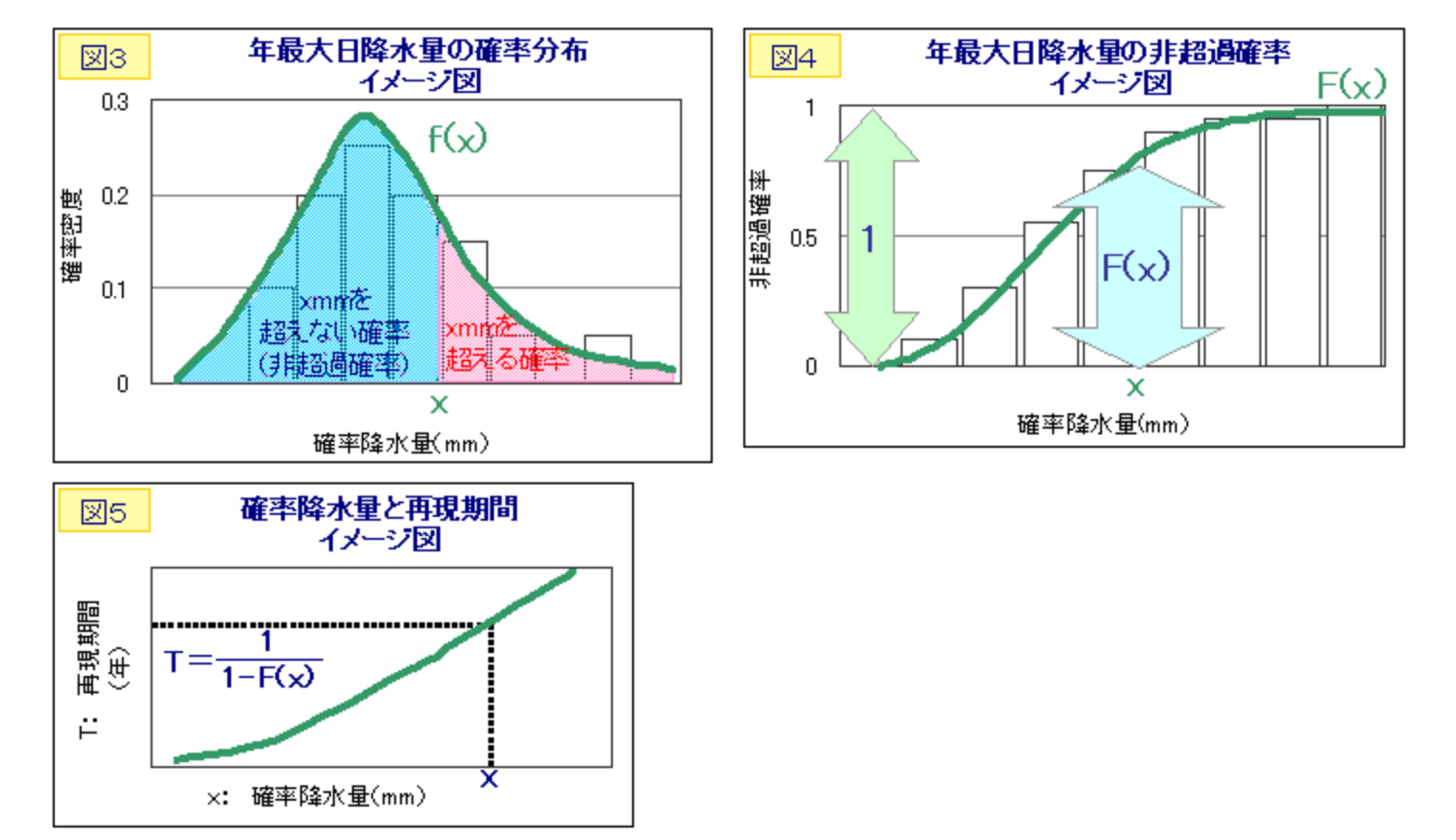
以下、上記出典から得た参考図(説明は省略)