GPS位置情報ビッグデータによる人口分布の高解像度化と接触頻度の推定

概要

　新型コロナウイルス感染者の減少後の経済再開局面では、感染再拡大と経済的損害の両方を抑えることが求められる。どちらも、他者との接触頻度と直結しており、両立するには、接触頻度の目標を定め、接触頻度を精度高く高頻度でモニタリングする必要がある。本稿では、接触頻度を高精度に推計する手法を提案する。高精度のメッシュ型人口分布と整合性を維持しつつ、高解像度のGPS型人口分布をオーバーサンプリングすることにより、高精度で高解像度の人口分布を生成する。これにより、人口密度の変化による（単位時間あたり）一人あたりの接触人数の変化が推定でき、人口減と一人あたりの接触人数減の両要因を考慮した接触頻度の減少を推計する。分析の結果、55％の人口減で、接触の頻度は約8割減少する。4月時点における、主要駅周辺での人口減は6割から8割であるが、接触の密度効果を考慮すると、接触頻度は既に8割から9割5分減少している。

1. はじめに

　2019年末に中国の武漢で発生したコロナウイルス感染症は、世界中に広がり、現在（2020年5月6日）までに、全世界で358万人以上が感染し、25万人以上の命が失われている。このパンデミックを止めるために、世界各国で外出禁止令が発動された。しかしながら、それにより経済活動が停滞し、第1四半期のGDPは中国では前年比6.8％減、米国では前期比で4.8％減となっており、欧州委員会はユーロ圏での落ち込みが過去最大となる前年比7.7％減を予想している[1]。新型ウイルスによる経済的影響が深刻化する中、封鎖措置の緩和と経済損失の抑制への圧力が世界各国で強まっている。

　日本においては、4月7日に政府が7都府県を対象として緊急事態宣言を出した。安倍首相はコロナウイルスの感染予防のために、人と人との接触頻度を、最低7割、極力8割削減するよう呼びかけた [2]。4月16日には、感染のまん延が7都道府県（東京都、神奈川県、千葉県、埼玉県、大阪府、兵庫県、福岡県）と同等な6都道府県（北海道、茨城県、石川県、岐阜県、愛知県、京都府）を対象に加え特別警戒都道府県と位置づけた[3]。5月4日には、緊急事態宣言を5月31日まで延長することを決定し、特定警戒都道府県については、引き続き極力8割の接触削減にむけたこれまでと同様の取り組みをおこなうと強調した[4]。世界と同様、接触削減は経済活動を停滞させており、日本経済も第2四半期のGDP成長率が戦後最悪になるとみられている[5]。

　他者との接触頻度と経済活動の度合いは直結している[6]。現在、経済活動が停滞しているのは、接触頻度に関する規制があるためであり、今後、この規制を緩めることができれば、経済活動は自然と活発になり停滞から脱出できる。しかし、経済活動の活性化は、他人との接触頻度を増大させ、感染拡大が懸念される。このウイルスは潜伏期間が長いために、感染状況をリアルタイムに把握するには、新規感染者数のモニタリングでは遅れてしまい、接触頻度で測る必要がある。これまでの感染拡大局面では、接触頻度は感染阻止のためだけに使われてきた。しかし、今後の経済再開局面では、実質GDPや失業率の数値目標に見合う接触頻度の目標を定めて、経済活動と感染阻止を両立していかなければならない。その実現には、接触頻度を精度高く高頻度で推計し、社会に提示することが必須である。

　一連の対策におけるキーワードは「接触頻度」であるが、この定義について厚生労働省コロナ対策本部クラスター対策班から5月1日に、「接触頻度＝人口×単位時間あたりの一人あたりの接触人数」と発表された[7,8]。また同時に、いくつかの繁華街について、一人がある1時間において接触する人数は同じと考えた場合の接触頻度が、平時（1月17日と19日）と非常時（4月24日と26日）で、どの程度変化したかについて示され、8割削減が達成されていないと述べられた。

　接触頻度の定義によると、（単位時間あたりの）一人あたりの接触人数を考慮する必要があり「接触頻度の変化率≠人口の変化率」である。しかしながら、報告[7,8]では、一人あたりの接触人数を一定と仮定し、「接触頻度の変化率＝人口の変化率」としている。人口密度の高い地区では一人が接触する人数が多くなることが考えられるが、そのような接触の密度効果について十分な情報がないためと説明されている。

　本稿では、許諾されたGPS位置情報ビックデータを応用することで、携帯電話の基地局情報により、日々、高精度に見積もられるメッシュ型人口分布を高解像度化する。これにより、各個人の接触人数を数え上げることが可能になり、人口密度低下による一人あたりの接触人数の減少の効果を、接触頻度の変化率に反映させることができる。この方法を用いれば、日々の接触頻度を高精度に推計することが可能である。推計の結果、主要な繁華街において、4月時点の人口減は6割から8割であるが、接触の密度効果を考慮すると、接触頻度は既に8割から9割5分減少していることがわかった。

　以降の節では、第2節において、本研究で利用する高精度なメッシュ型人口分布、高解像度のGPS型人口分布について説明する。第3節では、クラスター対策班によって示された、一人あたりの接触人数を一定とした場合の接触頻度の変化率は、人口の変化率と同じであること示す。第4節では、高精度なメッシュ型人口分布に、高解像度のGPS型人口分布を反映させてSVM-SMOTEアルゴリズム[9]でオーバーサンプリングすることにより、高精度で高解像度の人口分布を生成する。高精度で高解像度の人口分布から各人の（単位時間あたりの）接触人数を数え上げることで接触頻度を推定する手法を説明する。第5節では、特別警戒都道府県にある繁華街について接触頻度を推定し、平時と非常時で接触頻度の変化を示す。第6節は、まとめと課題である。

2. 人口分布データ

　本稿では、メッシュ型人口分布とGPS型人口分布の二種類の人口分布データを用いる。メッシュ型人口分布データについては、株式会社ドコモ・インサイトマーケティングが提供する国内人口分布統計（リアルタイム版）モバイル空間統計®[10]を利用する。モバイル空間統計では、日本を500m×500m四方のメッシュに分割し、約7800万台のドコモの携帯電話から推計された各メッシュの1時間ごとのリアルタイム人口が表示される。サンプルサイズが大きいので、人口分布の精度が高いのが利点である[11]。本稿では、2020年1月17日（金）と1月29日（日）、4月24日（金）、4月26日（日）のデータを使って分析した。

　GPS型人口分布データとしては、株式会社Agoopが提供するポイント型流動人口データ[12]と、ソーシャル・ネットワーキング・サービスの1つであるTwitterの書き込みに付与された正確な位置情報を利用する。ポイント型流動人口データは、スマートフォン向けアプリケーションを通じて、許諾を得たユーザーから30分毎に集められた約21万台のスマートフォンのGPS位置情報（緯度、経度）である。地理的な誤差が10m以内の位置情報のみを利用する。サンプルサイズが小さいが、人口分布の解像度が高いという利点がある[11]。2014年8月（12日から15日までのお盆の時期を除く）のデータを使って分析した。

　分析結果の頑強性を確認するために、ポイント型流動人口データと同じ分析を、Twitterの書き込みに付与された正確な位置情報（緯度、経度）に対してもおこなう。Twitterでの正確な位置情報は全ての書き込みの約5%に付与されている。2014年3月から2015年4月までの約1億3千万件の位置情報付き書き込みを利用する。日本においては、iPhoneからの書き込みが約50%を占めており、iPhoneのGPSの誤差は概ね10m以内である。移動者の位置情報を機種による誤差なく観測するために、iPhoneからの書き込みに付随する位置情報（緯度、経度）のみを分析する。Twitterの位置情報でも人口分布が再現できることが知られている[13]。

3. 接触頻度の変化率（一人あたりの接触人数＝一定）

　ある地域hにいる人口k_h人が、一人あたりn_h人と接触すると、その地域の合計の接触頻度t_hは、

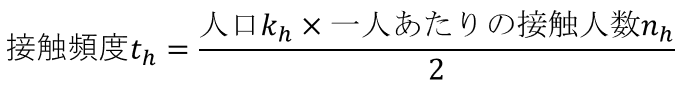
である。例えば、「Aさん、Bさん、Cさん、Dさん」の4人しかいない場面では、「AーBペア、AーCペア、BーDペア、CーDペア」のように、各人が単位時間あたり2人と接触していると、合計の接触頻度はペアの数 (4×2)/2＝4回である。

　2020年5月1日の厚生労働省コロナ対策本部クラスター対策班の報告では、一人あたりの接触人数が人口密度に依存せず、混んでいる場合も空いている場合も一定であるとして、平時と比べた非常時の接触頻度の変化率を算出した。つまり、地域の人口が減り、人口密度が変化しても一人あたりの接触人数は一定のままで時間に依存しない。従って、地域hの接触頻度の変化率は、

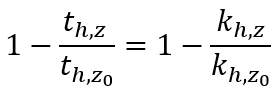
となり、人口の変化率と等しい。ここで、t_{h,z0}とk_{h,z0}は基準となる日時z0における地域hの接触頻度と人口であり、t_{h,z}とk_{h,z}は変化観測の対象となる日時zにおける地域hの接触頻度と人口である。従って、この計算では、その地域の人口が1/2になると、接触頻度も1/2になる。

　図1（a）は、クラスター対策班が示した1月19日と4月26日を比較した渋谷駅周辺の8時台から15時台の接触の変化率である。一方で、（b）はメッシュ型人口分布を用いて算出した同じ2時点間の人口の変化率である。ここでは、データ利用の都合で、渋谷区内のみ算出した。図1（a）と（b）が完全に一致していることが読み取れる。つまり、クラスター対策班から公表された値は、人口減少率であり、人口密度の低下に伴う一人あたりの接触人数が減少する効果が反映されていない。この結果、接触頻度の減少が過小評価されている可能性がある。政府は国民に対し「接触頻度の8割削減」を呼び掛けているが、その接触頻度の測定が正確でない可能性がある。

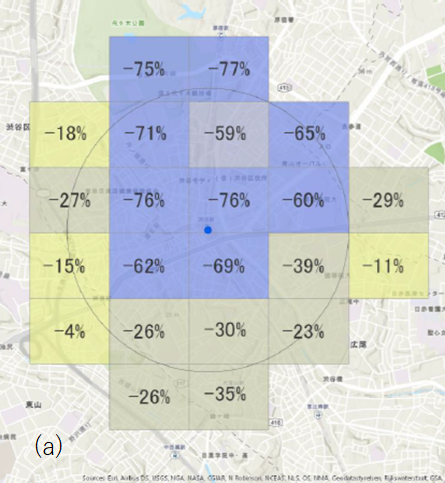
図1（a）クラスター対策班が示した1月19日と4月26日を比較した渋谷駅周辺の8時台から15時台の接触の変化率 [5]

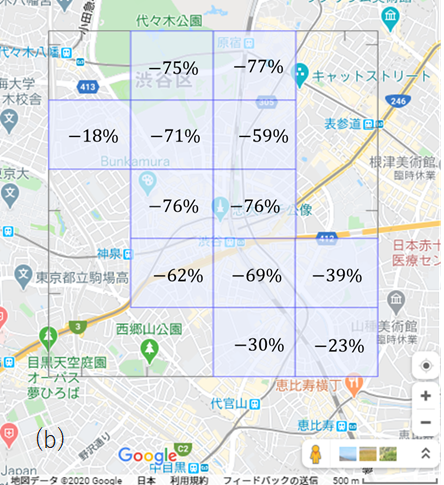
図1（b）メッシュ型人口分布から算出した人口の変化率

4. 高精度で高解像度の人口分布の生成による接触頻度の推定法

　本節では、図2に示すように、高精度のメッシュ型人口分布と整合性を維持しつつ、高解像度のGPS型人口分布をオーバーサンプリングし、高精度で高解像度の人口分布を生成する。その上で、各人の2m範囲を接触半径と定義し、各人の接触人数を数え上げる。平時の渋谷のスクランブル交差点や原宿の竹下通りは過密であり、各人は多くの人と接触する。一方で、住宅の多い地域では人影はまばらであり、各人は、ほとんど人と接触しない。非常時になると、スクランブル交差点も竹下通りも、人がまばらで、各人は、ほとんど人と接触しなくなる。このようにして、接触頻度に、人口の減少だけではなく、一人あたりの接触人数の減少を反映させる。 　図2の左図は、メッシュ型人口分布から観測された2020年1月17日の渋谷駅周辺の9時台から17時台の平均人口である。約3千人から3万人の範囲で分布している。図2の中央の図は、平日の9時台から17時台の人々の位置情報である。同一人物が異なる日時に位置情報を報告した場合も全て描画している。これにより、我々は、渋谷周辺の平日の人々の位置の標準的な空間分布を知ることができる。株式会社Agoopのポイント型流動人口データでは、2014年8月の（お盆を除く）平日の位置情報をメッシュ毎に集計すると約1千から5千件の範囲で分布している。位置情報付きTwitterデータでは、2014年3月から2015年4月の平日の位置情報をメッシュ毎に集計すると約2千から2万件の範囲で分布している。

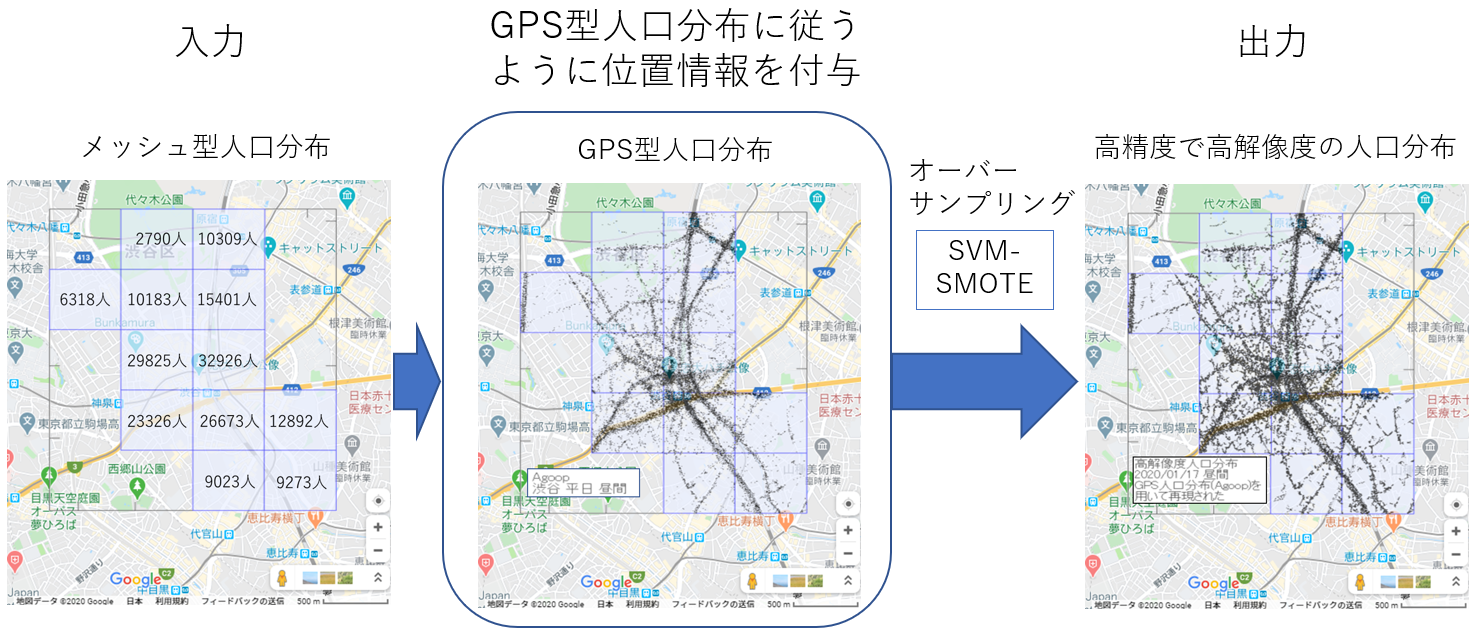
図2　高精度で高解像度の人口分布を仮想生成する手順

　ポイント型流動人口データと位置情報付きTwitterデータから得られるGSP型人口分布の違いについて述べる。図3は平日昼間の位置情報付きTwitterデータから得られるGSP型人口分布である。図2中央の図のポイント型流動人口データと同様に、繁華街や道沿いに位置情報が集中している一方で、建物内での位置情報の多さが目立つ。これは、目的地で足を止めてTwitterに書き込む行動を反映していると思われる。つまり、位置情報付きTwitterデータから得られるGPS型人口分布は、目的地に重みがかかった人口分布であると考えられる。

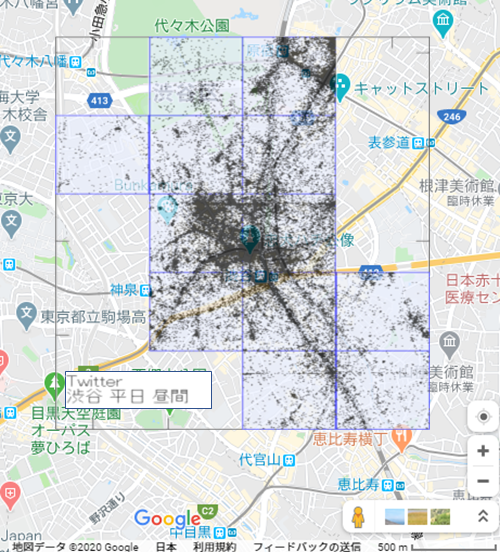
図3 2014年3月から2015年4月の平日の9時台から17時台の位置情報つきTwitterの位置情報

　次に、メッシュ毎にGPS型人口分布を、メッシュ型人口分布の人数まで、SVM-SMOTEアルゴリズムを用いてオーバーサンプリングする。SMOTE（Synthetic Minority Over-sampling Techique）の手順は以下のとおりである[14]。

（1）あるメッシュの中の位置情報をランダムに1つ選ぶ。（図4ではx1）
（2）x1から近い順に近接の位置情報をk個（例：k＝4）用意する。（図4ではx11～x14）
（3）位置情報x11～x14の中からランダムに1つ選ぶ。（図4ではx11）
（4）位置情報x1とx11を結んだ直線上にランダムに新しい位置情報を内挿する。(図4ではr1)

　この（1）から（4）の手順を繰り返すことにより、高解像度のGPS人口分布の形状を変えずに、位置情報を高精度のメッシュ型人口分布と同じ人数まで増やしていく。SVM-SMOTEではサポートベクトルにより位置情報をクラスタリングし、サポートベクトルを超えて新しい位置情報の内挿がおこなわれないようにする[9]。図2の右図は、SVM-SMOTEによって位置情報を増やすことによって生成された高精度で高解像度の人口分布である。

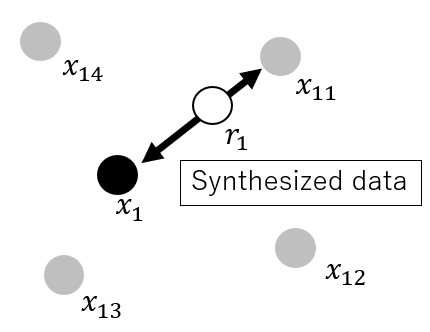
図4　SMOTEの概念図

　次に、オーバーサンプリングにより生成された高精度で高解像度の人口分布から、接触頻度を計測する。接触範囲を2m以内であると仮定して、500mメッシュを4m×4mの15,625ブロックに分割する。ブロック内の人々は相互に接触があるとすると、ブロックb内のk_b人の間の合計の接触頻度t_bは、

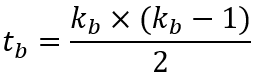
である。したがって、ブロック内の人口が1/2になると、接触頻度は約1/4になる。第3節では500mメッシュで調べていたため、一人あたりの接触人数を定数として大雑把な近似をしてしまっていたが、ここでは空間的な解像度を上げて4m×4mのブロックで調べることにより、一人あたりの接触人数の高精度な推定が可能になっている。

　ブロックb内では、全員と接触があるので、一人あたりの接触人数はn_b=k_b-1である。メッシュhにおける接触頻度t_hは、

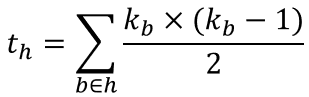
で求まる。最後に、メッシュhにおける一人あたりの接触人数n_hは、

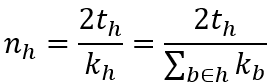
で算出できる。

5. 接触頻度の変化率（一人あたりの接触人数≠一定）

　第4節の手法を用いて、渋谷周辺の休日について、平時（1月19日）と非常時（4月26日）の9時台から17時台の接触頻度を算出し、接触頻度の変化率を人口の変化率とあわせて図5で示す。休日の渋谷駅周辺の人口は70％台で減少しており、人口減のみでは8割減は達成していない。しかしながら、人口密度が低下したことによる（単位時間あたり）一人あたりの接触人数の減少も考慮すると、接触頻度は90％台の減少になり、政府の掲げる目標である接触頻度の8割減を達成していることになる。駅周辺から少し離れた住宅のあるメッシュでは、人口減は数十％であり小幅であるが、接触頻度では50%近い減少となる。多くの接触は、駅近辺で発生するため、これらの地域全体では、人口減が69%、接触頻度減は90%である。

　図6は、平日の結果を示している。渋谷駅周辺の人口減は60％程度であるが、接触頻度では人口密度の低下が寄与して80％を超えており、接触頻度8割減をクリアできている。駅周辺から少し離れても60％近い接触頻度減が達成されている。平日も、これらの地域全体では、人口が59%減り、接触機会は85%減少している。

　図5と図6の（b）（c）が示すように、上記の分析結果は、ポイント型流動人口データによる高解像度化でも、位置情報付きTwitterデータによる高解像度化でも変わらない。つまり、渋谷駅周辺は、平日も休日も接触頻度8割減が達成されている。

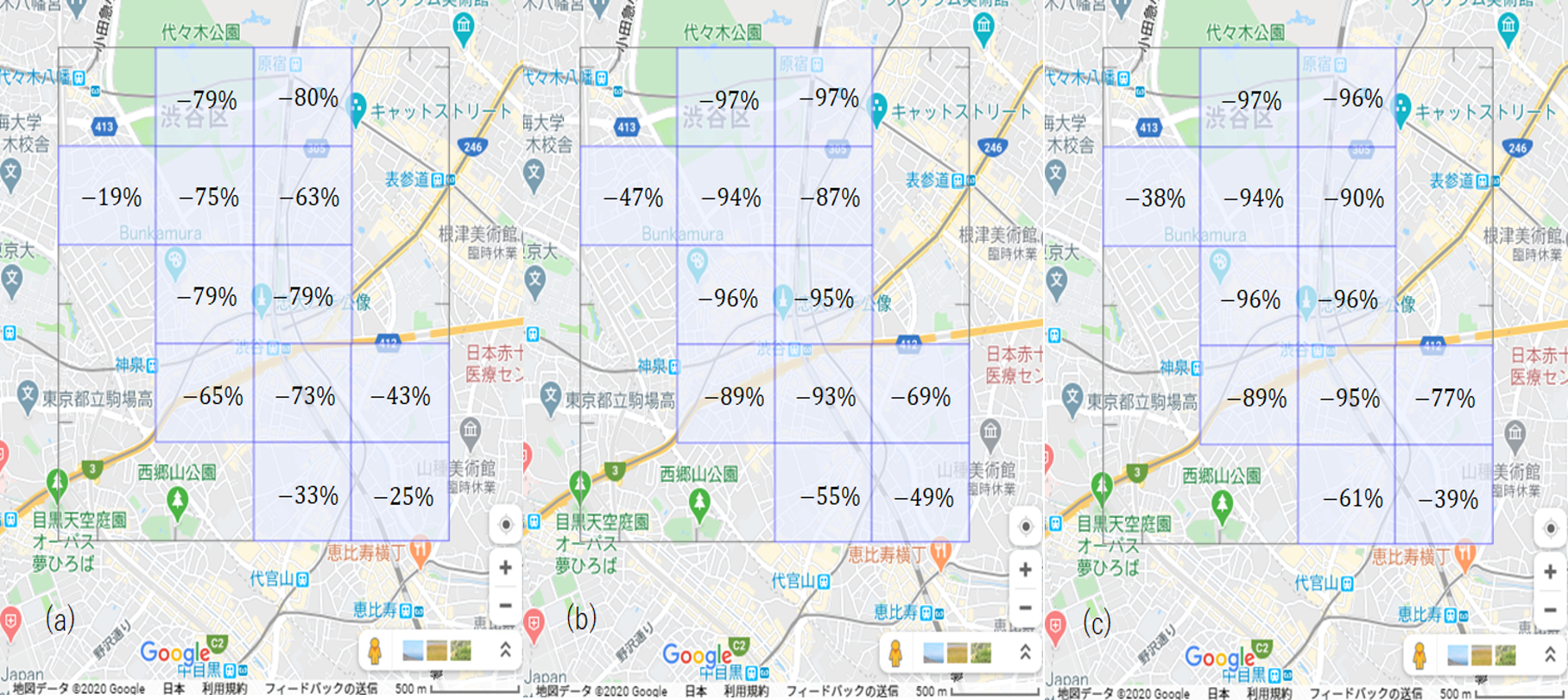
図5　渋谷周辺の休日の昼間（9時台から17時台）における平時（1月19日）と非常時（4月26日）の比較（a）人口の変化率、（b）接触頻度の変化率（ポイント型流動人口データによる高解像度化）、（c）接触頻度の変化率（位置情報付きTwitterデータによる高解像度化）

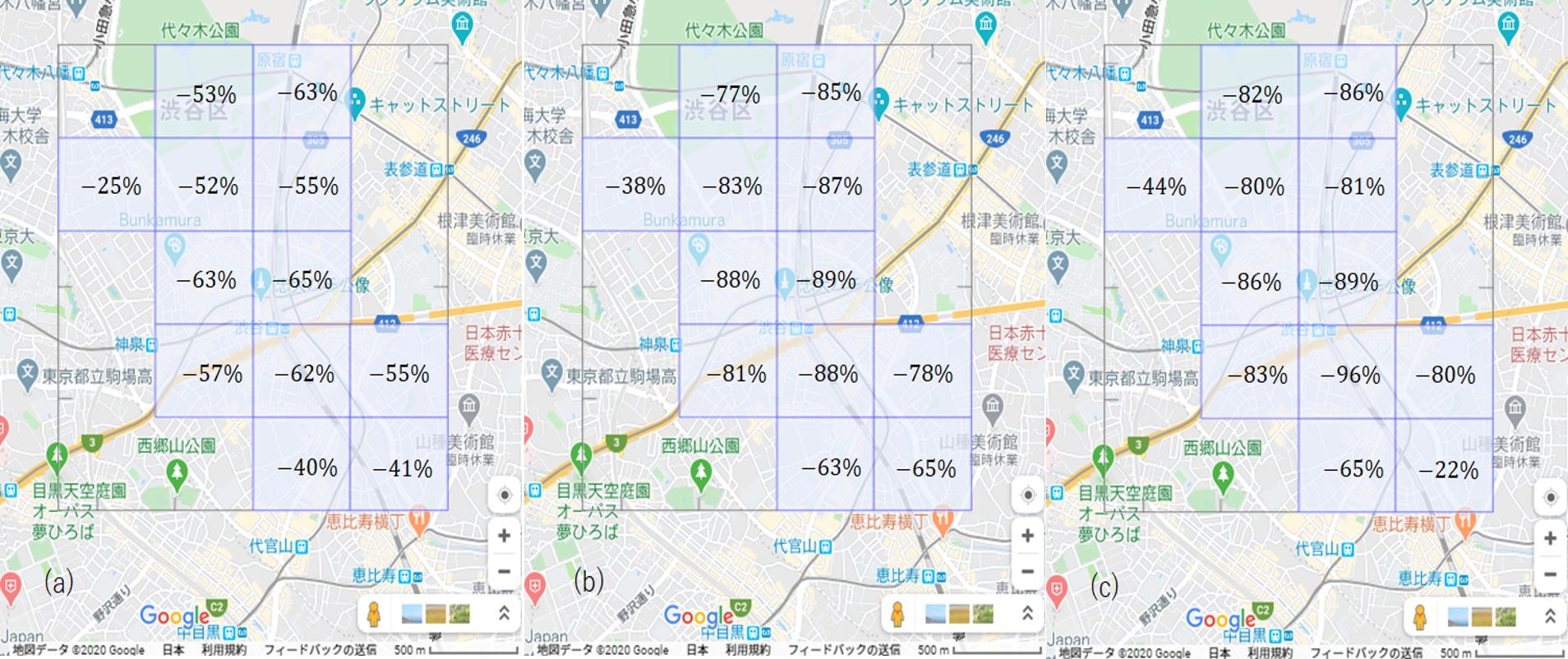
図6　渋谷周辺の平日の昼間（9時台から17時台）における平時（1月17日）と非常時（4月24日）の比較（a）人口の変化率、（b）接触頻度の変化率（ポイント型流動人口データによる高解像度化）、（c）接触頻度の変化率（位置情報付きTwitterデータによる高解像度化）

　次に、特別警戒都道府県にある主要駅周辺の人口減と接触頻度減を測定する。表1は、位置情報付きTwitterデータによって高解像度化した人口分布から算出した人口減と接触頻度減の結果である。人口減は平日が約6割、休日が約7割減である。しかしながら、接触頻度で測定すると、平日でも、ほとんどの主要駅周辺で8割減が達成されており、休日においては9割以上の接触頻度減が達成されている。図5と図6、表1の結果から、約55％の人口減に達すると、人口密度の減少により一人あたりの接触人数が抑制され、接触頻度8割減が達成されていることが分かる。

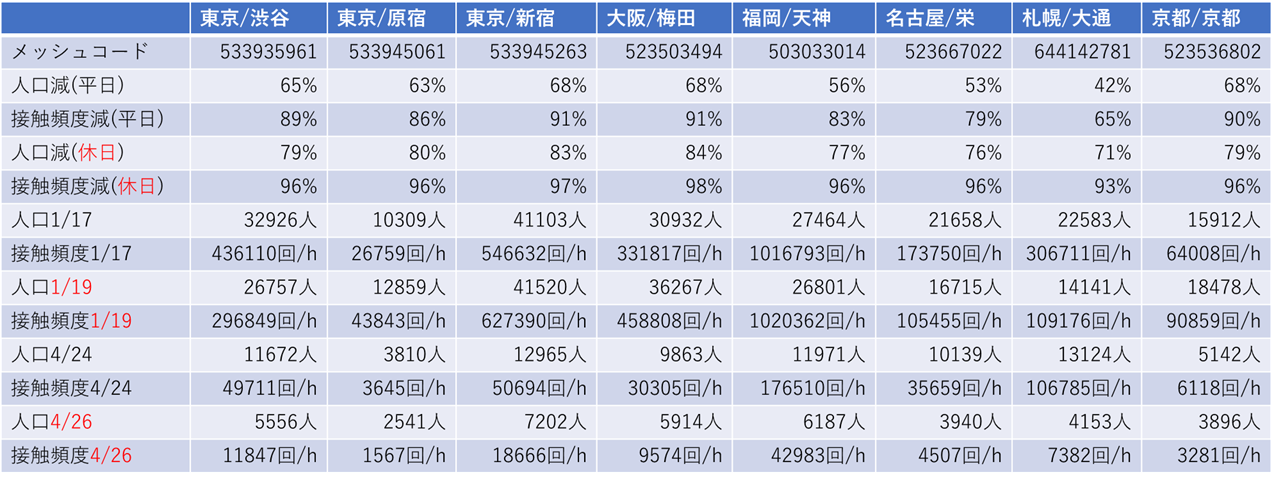
表1　全国各地の繁華街にある駅周辺における平時（1月17日、19日）と非常時（4月24日、26日）の人口及び接触頻度の比較。位置情報付きTwitterデータによって高解像度化された人口分布から推定。メッシュコードが表す座標（緯度、経度）については総務省統計局「地域メッシュ統計」を参照[15]

6. まとめと課題

　地域における接触頻度の減少は、人口の減少と、一人あたりの接触人数の減少の2つの要因によって起きる。5月1日の厚生労働省コロナ対策本部クラスター対策班の報告では、接触頻度の推定に際して、一人あたりの接触人数の減少が考慮されていなかった。本稿では、高精度のメッシュ型人口分布と整合性を維持しつつ、高解像度のGPS型人口分布をオーバーサンプリングし、高精度で高解像度の人口分布を生成した。これにより、人口密度の変化による（単位時間あたり）一人あたりの接触人数の変化が推定でき、人口減と一人あたりの接触人数減の両要因を考慮した接触頻度の減少を計測した。約55％の人口減で、接触頻度は8割減少していた。特別警戒都道府県にある多くの主要駅周辺では、人口は8割減少していないが、接触頻度は8割以上減少しているという結果を得た。

　本稿では、人々の空間的な詳細な密度分布を知るためにGPS型人口分布を利用した。密度分布の主な特徴は時間的に大きくは変化しないが、駅や新たなランドマーク等ができると局所的には変化する。本稿で用いたのは、2014年のGPS型人口分布であり、最新ではない。接触頻度の推定精度を高めるには、メッシュ型人口分布データと同日に取得されたGPS型人口分布データが必要である。また、本稿では、建物の高さを考慮しなかった。繁華街では、高層の建物が多く、異なるフロア間では接触は起こり得ないため、本稿での接触頻度の推計は過大になっている可能性がある。高さを考慮するためには、繁華街の建物情報が必要であり、建物情報を反映させることで、接触頻度の推定精度は向上すると思われる。

　新型コロナウィルス感染の収束のためには、接触頻度の8割削減が必要と言われている。しかし、接触頻度の削減は人々の移動の自由を制限し、経済的な損失を生むことを忘れてはならない。コロナウイルスとの戦いの長期化が予想される状況にあって、健康の被害と経済的損害の両方を抑えることが求められている。そのためには時々刻々と変化する状況を正確かつ迅速に把握し、人々に知ってもらうことが不可欠である。本稿の分析対象である「接触頻度」は人々が知るべきキー変数のひとつであろう。各地の接触頻度の状況を、日々、ビッグデータを用いて見える化することによって、我々は過度な自粛をせずに、可能な範囲で経済活動をおこなうことが可能になるだろう。また、4m四方の狭い範囲で平均的な接触頻度を推定できるため、例えば、通勤経路を変えた場合に、接触頻度をどの程度減らせるのか見積もることができる。これを応用すれば、接触機会を減らすアドバイスをするAIも作れるであろう。本研究は、コロナ時代の社会経済活動を科学的にサポートできるであろう。

謝辞

　本研究の一部は、科学研究費補助金19K22852、16H02872のサポートを受けている。本稿で用いた国内人口分布統計（リアルタイム版）モバイル空間統計®は株式会社ドコモ・インサイトマーケティングから提供を受けました。感謝を申し上げます。

参考文献

[1] European Commission "Spring 2020 Economic Forecast: A deep and uneven recession, an uncertain recovery". https://ec.europa.eu/commission/presscorner/detail/en/ip_20_799 （2020年5月7日アクセス）
[2] https://www.kantei.go.jp/jp/98_abe/statement/2020/0407kaiken.html（2020年4月20日アクセス）
[3] https://www.kantei.go.jp/jp/98_abe/actions/202004/16corona.html（2020年4月20日アクセス）
[4] https://www.kantei.go.jp/jp/98_abe/actions/202005/04corona.html (2020年5月7日アクセス）
[5] 日本経済新聞「マイナス21% 成長予想 4～6月民間平均、戦後最悪に」（2020年4月30日）https://www.nikkei.com/article/DGXMZO58680170Q0A430C2MM8000/ （2020年5月7日アクセス）
[6] Martin S. Eichenbaum, Sergio Rebelo, and Mathias Trabandt. The macroeconomics of epidemics. No. w26882. National Bureau of Economic Research, 2020.
[7] 新型コロナウイルス感染症対策専門家会議「新型コロナウイルス感染症対策の状況分析・提言」（2020 年 5 月 1 日）https://www.mhlw.go.jp/content/10900000/000627254.pdf (2020年5月7日アクセス）
[8] 厚生労働省コロナ対策本文クラスター対策班「2020年5月1日の専門家会議での報告内容の捕捉」（2020年5月1日）https://github.com/contactmodel/20200501/blob/master/0501_public.pdf （2020年5月7日アクセス）
[9] A. Fernández, S. Garcia, F. Herrera, and N. V. Chawla. SMOTE for learning from imbalanced data: progress and challenges, marking the 15-year anniversary. Journal of artificial intelligence research 61, 863-905, 2018.
[10] 国内人口分布統計（リアルタイム版）モバイル空間統計®
[11] 菅愛子、 飯島信也、 兵頭大史、 藤原直哉、 水野貴之、 松本裕介、 武藤杏里、 瞿雪吟、 伊藤武真、 松井伸司、 五十嵐盛仁、 上田聖。東京都における流動人口データの有効性の検証. 総務省統計委員会担当室ワーキングペーパー、 2019-WP03、 2019。
[12] ポイント型流動人口データ https://www.agoop.co.jp/floating-population/（2020年5月7日アクセス）
[13] 水野貴之。ビッグデータによって変わる未来の公的統計。社会と調査 (2019) No.22,、pp.36-44、2019。
[14] N. V. Chawla, K. W. Bowyer, L. O. Hall, and W. P. Kegelmeyer. SMOTE: synthetic minority over-sampling technique. Journal of artificial intelligence research 16, 321-357, 2002.
[15] 総務省統計局「地域メッシュ統計」http://www.stat.go.jp/data/mesh/index.html （2020年5月7日アクセス）

注釈

「モバイル空間統計」は、株式会社NTTドコモの登録商標です。