ダイナミックな太陽活動が過去の気温上昇をもたらした？

「太陽から地球に届くエネルギーの量は，過去100年の間ほとんど変化していない。したがって，太陽活動は地球温暖化にほとんど寄与していない。」二酸化炭素（CO₂）排出が引き起こす地球温暖化の評価は，このような仮定に基づいている。しかしながら，最近のレビュー論文^{注1) ，注2)}によると太陽活動と地球温暖化を巡る論争は現在も継続している。

1．太陽エネルギーは今も昔も変わらない？

地球の平均的な気候は、太陽から届く光のエネルギーの量で決まる。太陽の光が地球の大気表面に垂直に入射するエネルギーは、すべての波長域の放射を合わせると約1361Wm^-2であり、これを太陽総放射量（TSI: Total Solar Irradiance）という。1750年から2019年までのCO₂による温室効果がおよそ2Wm^-2であることを考えると^注3)、TSIがわずかに変化しただけでも地球の気温が変わってしまうように感じる。しかしながら、実際にはTSIは長期的にはほとんど変化しないといわれている。

よく知られている太陽黒点（太陽表面に強い磁場がまとまって存在している領域^注4)）の数の変化に伴うTSIの変化が地球の気温に及ぼす影響を試算してみよう。太陽活動が活発化すると、黒点は広がりその数も増え、さらに黒点を取り囲むように非常に明るい白斑が多数出現する。黒点数の増減は約11年の周期で観測されることがよく知られており（図1）、年平均TSIの振幅はおよそ1Wm^-2である。この振幅を4で除して地球表面への平均入射量に換算し、地球の平均的な太陽放射の吸収率である0.7を掛けると^注5)，放射強制力の増加（減少）分である∆Fは0.175Wm^-2である。最新の「気候変動に関する政府間パネルの第6次評価報告書 自然科学的根拠（IPCC AR6 WG1）」による知見^注6)を参考にすると、温室効果ガス濃度が70年かけて倍増した場合の70年目の気温上昇（過渡的気候応答：TCR）を1.4～2.2℃、CO₂濃度が倍増したときの放射強制力F_2𝓍を3.71Wm^-2とすると、黒点数の増加（または減少）に伴う気温上昇（または減少）の量は、次のように推計される：

∆T=TCR∙∆F/F_2𝓍 = [1.4~2.2]×0.175/3.71=[0.07~0.1]℃

すなわち、地球の気温は最大でも0.1℃しか変動しない。このためTSIは「太陽定数（Solar Constant）」とも呼ばれ^注7)、気象学では太陽活動が及ぼす気候への長期的な影響は小さいというのが常識となっている。

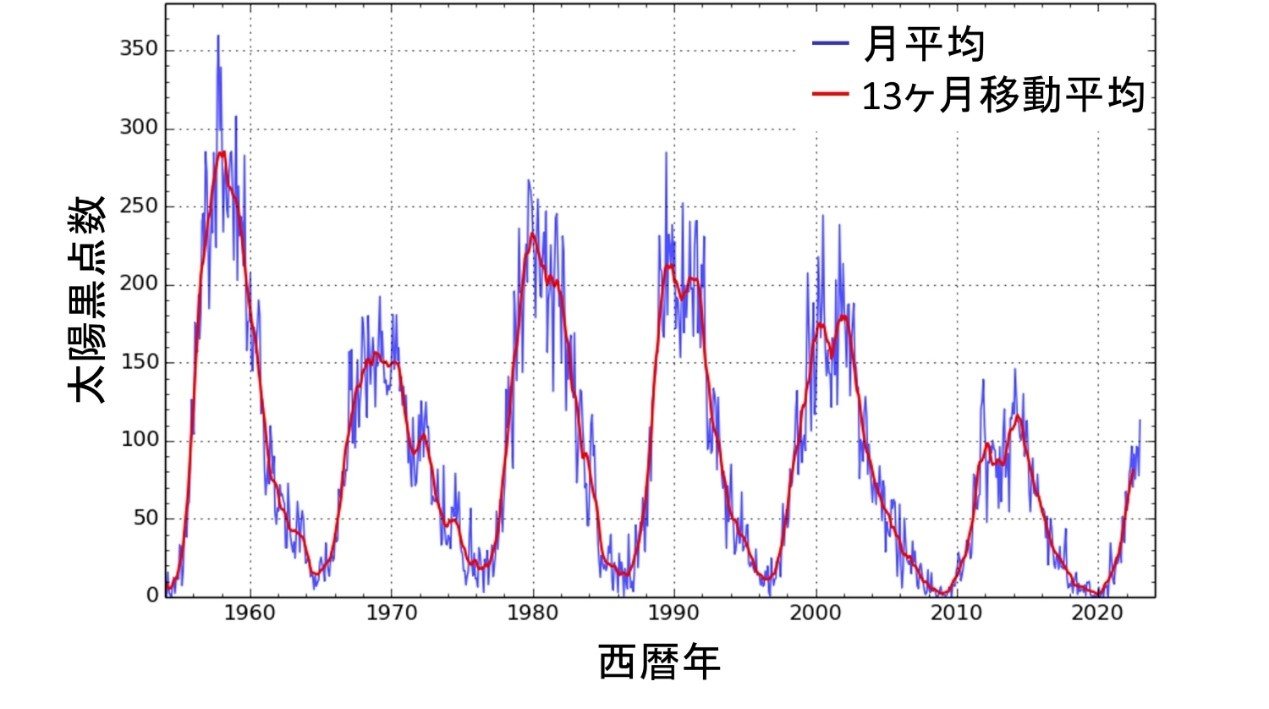
図1　1954年～2023年における太陽黒点数の月平均値および13ヶ月移動平均値の観測結果^注8)。

2．衛星観測時代の太陽活動に関する論争

ところが、実のところ「太陽定数が本当に定数とみなせるかどうか」はまだわかっていない。太陽の光は大気によって強く散乱してしまうために地上からの正確な計測は難しく、現在最も精度の高いTSIのデータを提供しているのは人工衛星である。図2aに示すように、1978年以降は米国航空宇宙局（NASA）の地球観測衛星であるACRIM(Active Cavity Radiometer Irradiance Monitor)による観測データが存在するが、ここに論争がある。人工衛星の寿命に対して太陽活動の周期が約11年と長いので、数年おきに衛星を打ち上げてデータの取得を継続していかなければならない。しかしながら、1986年1月に起きたスペースシャトル・チャレンジャー号の爆発事故によって衛星が打ち上げられず1989年6月から1991年10月の間が空白期間（ACRIM gap）になってしまったためである。

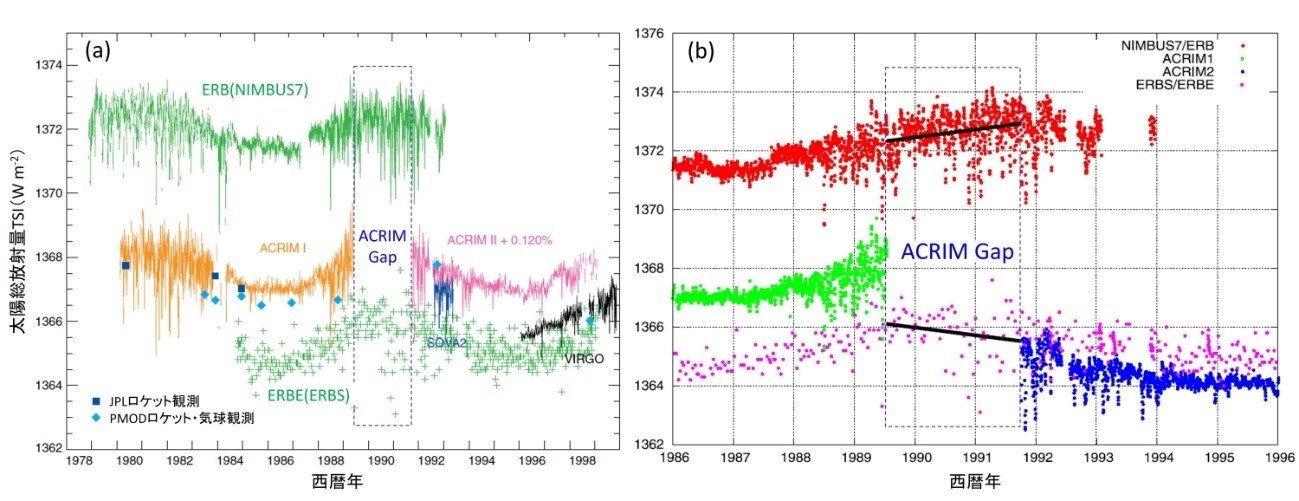
図2　(a)1979～1999年における様々な人工衛星・ロケット・気球観測による太陽総放射量（TSI）^注9)と1986～1996年におけるACRIM1・ACRIM2・ERBおよびERBEによる観測結果の経年変化^注10)。(b)の黒線はACRIM-Gap期間におけるERBおよびERBSの線形回帰直線。

この時期には、同じくNASAのERBE（Earth Radiation Budget Satellite）やERB（Nimbus 7 Earth Radiation Budget）という別の衛星が存在するので、これらのデータからTSIを推測する以外にない。しかしながら，2つの衛星の測定精度はACRIMに比べて劣ることと、測定器の違いにより同時期のTSIの変動傾向が異なることが問題を複雑にしている。ACRIM gapの期間も、両者の変動傾向は明らかに異なる。すなわち、ERBではTSIが1年あたり+0.27Wm^-2で増加していたのに対し、ERBSは1年あたり–0.27Wm^-2の減少と真逆の傾向が見られる（図2b：黒線）。

2つの衛星の違いをどのように解釈するべきか？そして、ACRIM gapにおけるもっともらしいTSIの変化はどのように表現するのが適切なのか？ACRIM^注11)とPMOD^注12)と呼ばれる2つの大きな研究グループの間で、今も論争が続いている。図3に示すように両者ともに太陽黒点の約11年周期変動は見られるが、ACRIMではTSIの極小値が1986年頃から1997年頃にかけて0.04%増加^注10)しているのに対して、PMODはわずかに減少している。両者の違いは、使用している衛星の組み合わせが異なることやこの期間に観測されている太陽黒点数の極小値の減少傾向（図1）を考慮するかどうかなどで生じている。

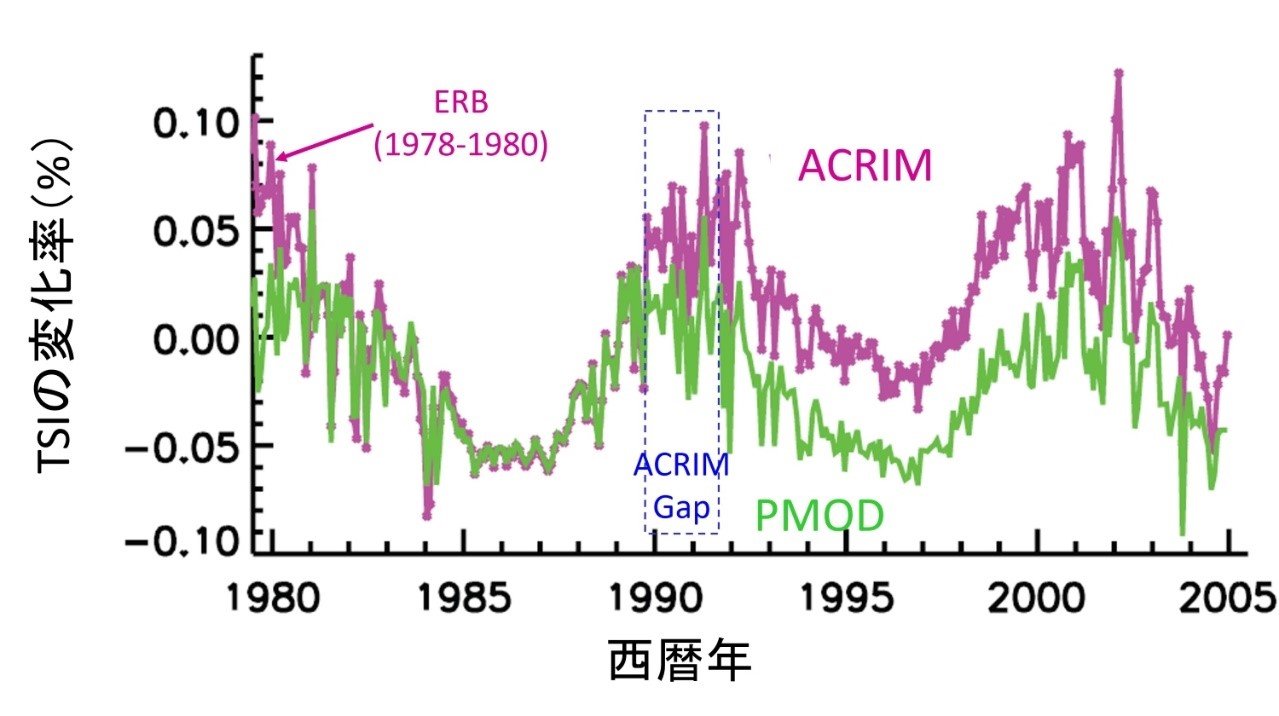
図3　1980年～2005年の平均値を基準としたACRIMデータセット^注11)およびPMODデータセット^注12)による月平均太陽総放射量（TSI）の変化率^注5)。1978年～1980年のACRIMデータセットはERBによる観測結果。

いずれの推定値が正しいのかを明らかにすることは、人為起源の地球温暖化量を評価する上で非常に重要である。仮にPMODが正しいとすれば、1980年以降の太陽定数は約11年周期を除けば「ほぼ定数」とみなすことができるので、この期間の太陽活動が及ぼす地球の気温上昇への影響は小さいと考えられる。逆に、ACRIMが正しいとすると、1985年頃のTSIが1995年頃には0.05%（約0.5Wm^-2）増加しており（図3：紫線）、2005年には低下するという数十年単位の変動を認めることになる。この変化量は前述した温室効果ガスの放射強制力（2Wm^-2）の4分の1に相当する。また、数十年単位の TSIの変動傾向は後述する地上気温の変動傾向と似ており、CO₂排出による地球温暖化の裏に太陽活動の影響があった可能性が出てくるのである。

3．過去300年の太陽総放射量に関する論争

1978年以前は衛星観測が存在しないので、衛星観測の変動傾向（図3）とその他のTSIに関係しそうな指標をベースにTSIの変化をモデル化するしかない。ここでも、前節のPMODとACRIMの関係と同じように、Low-variabilityモデルとHigh-variabilityモデルという2つのモデルが対立している。前者は衛星観測時代のPMODデータセットを参考に黒点数と白斑の観測記録に基づいたTSIのモデルである。これに対して、後者はACRIMデータセットを参考に、黒点数・白斑データだけでなくその他の指標（黒点の本影・半影の平均比率，黒点サイクルの長さ，太陽自転速度，波長10.7cmの太陽マイクロ波放射量の変動，プラージュ（羊斑と呼ばれる太陽の彩層の明るい領域）の面積、極白斑、黒点崩壊速度、太陽風の速度、地磁気活動度など^注13) ）のデータも含めて総合的に解析し、構築されたモデルである。

モデル名の「variability」は、数十年周期の変動を意味している。図4で示すように、過去300年間で見ると両者のTSIの変動幅が全く異なっているのがわかる。Low-variabilityモデルの結果には、太陽黒点の約11年周期と1700年からの緩やかな上昇傾向が見られる（図4：緑線）。これに対して，High-variabilityモデルにも約11年周期の変動に数十年周期単位の大きな変動が重なりつつ上昇している（図4：赤線）。このような大きな変動は、太陽黒点数や白斑以外の指標（データ）に見られる。

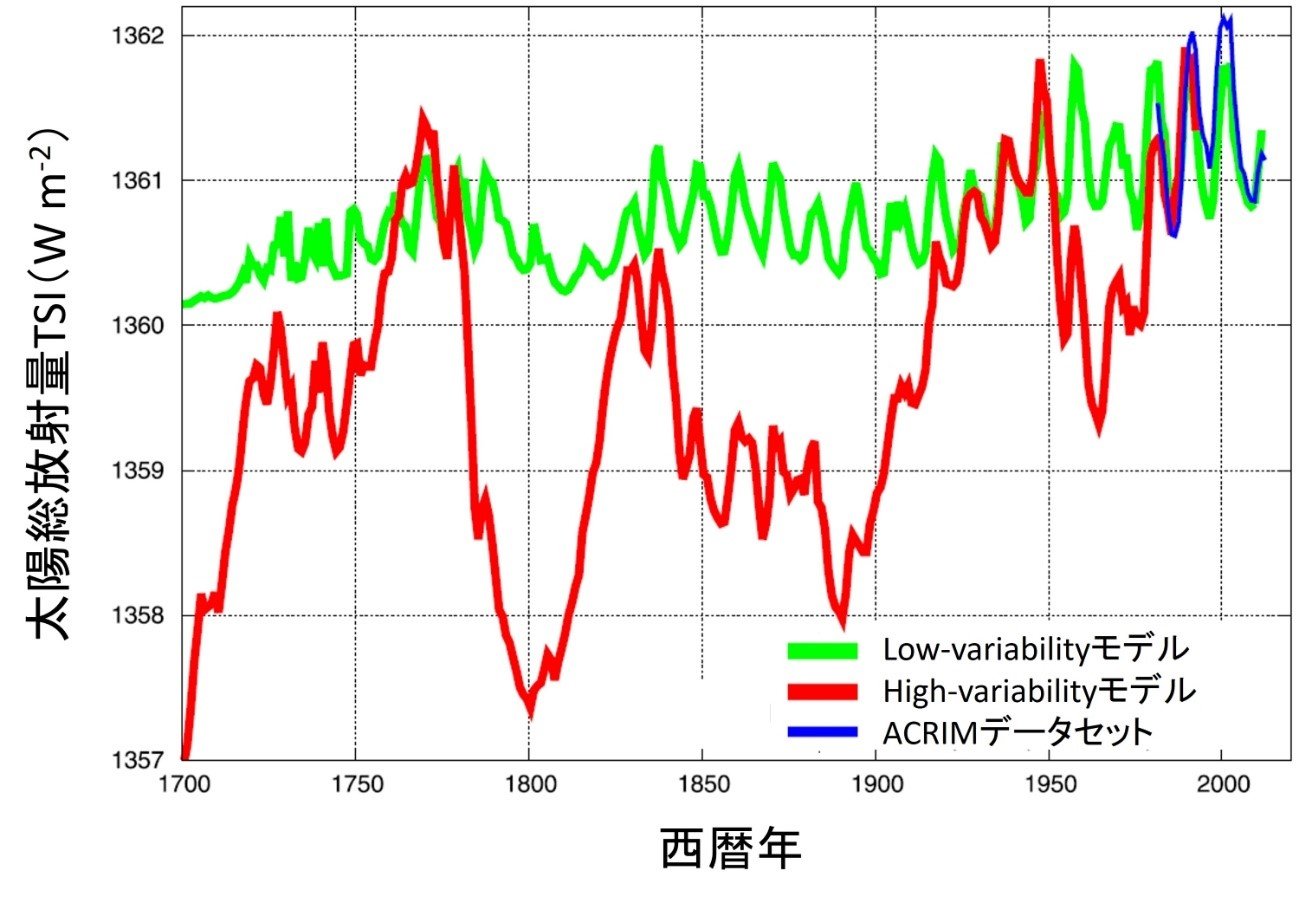
図4　1700年～2004年のLow-variabilityモデル（Kopp and Lean, 2011^注14) ）とHigh-variabilityモデル（Hoyt and Schatten, 1993^注15)の補正）による太陽総放射量（TSI）の推定結果とACRIMデータセットによる観測値の経年変化^注10)。

仮にHigh-variabilityモデルが正しいとすると、過去300年間の太陽定数を一定とみなすことは難しくなる。1700年は70年間にわたり太陽黒点が観測されなかった「マウンダー極小期」の終わりであるが、この年を基準にすると1770年頃、1820年頃、1940年頃、そして2000年前後に約4Wm^-2（放射強制力∆F=0.7Wm^-2に相当）もTSIが増加したことになるからだ。再び式(1)を用いると、1800年からのTSIの増加によって生じうる気温上昇量∆Tは

∆T=TCR∙∆F/F_2𝓍 = [1.4~2.2]×0.7/3.71=[0.26~0.42]℃

となり、過去の太陽活動によって地球気温が大きく上昇した可能性がある。

4．過去の気温上昇は太陽活動でも説明できる？

地球温暖化の速度を評価する上では、 過去の太陽活動（TSI）が実際の気温の変化にどの程度影響したのかが重要である。過去200年間を対象に、この影響を統計解析で調べた研究がある^注1)。この研究では、地上気温がTSIとともに比例すると仮定して、最小二乗法により地上気温のデータを縦軸のスケールを合わせてそれぞれのTSIのモデルで再現するようフィッティングした。そして、気温の上昇率に対してTSIの上昇率が何割であったかを評価した。この結果は、 TSIによって気温変動を説明できる割合（寄与率）の「最大見積もり」である。TSIのモデルには、IPCCの最新の報告書^注6)で推奨されているMatthes et al. (2017)^注16)のLow-variabilityモデル（図5a, b）と2つのHigh-variabilityモデル（図5a, b）を用いている。気温データには米国海洋大気庁による地球全体の地上気温データセット（GHCN：Global Historical Climatology Network）を用いているが、都市熱（ヒートアイランド）の影響を加味して^注17)、北半球における田舎のみの観測地点全て（図5a, c）と都市を含めたすべての観測地点全て（図5b, d）を平均した2つのデータセットを用いた。

図5がフィッティングの結果である。Low-variabilityモデルを用いた場合、田舎のみの地点における気温上昇率の15–27%（図5a）、全ての地点における気温上昇率の21–22%がTSIによって説明できる割合であり（図5b）、残りの割合はCO₂排出による気温上昇による^注1)。一方、High-variabilityモデルを用いた場合には、TSIの寄与率はそれぞれ95–98%、71–81%と大幅に増加した（図5c, d）。High-variabilityモデルのTSIと気温の変動パターンがよく似ているためである。1841年～2018年の田舎のみの地点の気温上昇率は100年間で0.44℃^注1)であり（図4c）、TSIのモデル選択によってはそのほぼ全てが太陽放射の数十年規模の変動で説明できることになる。

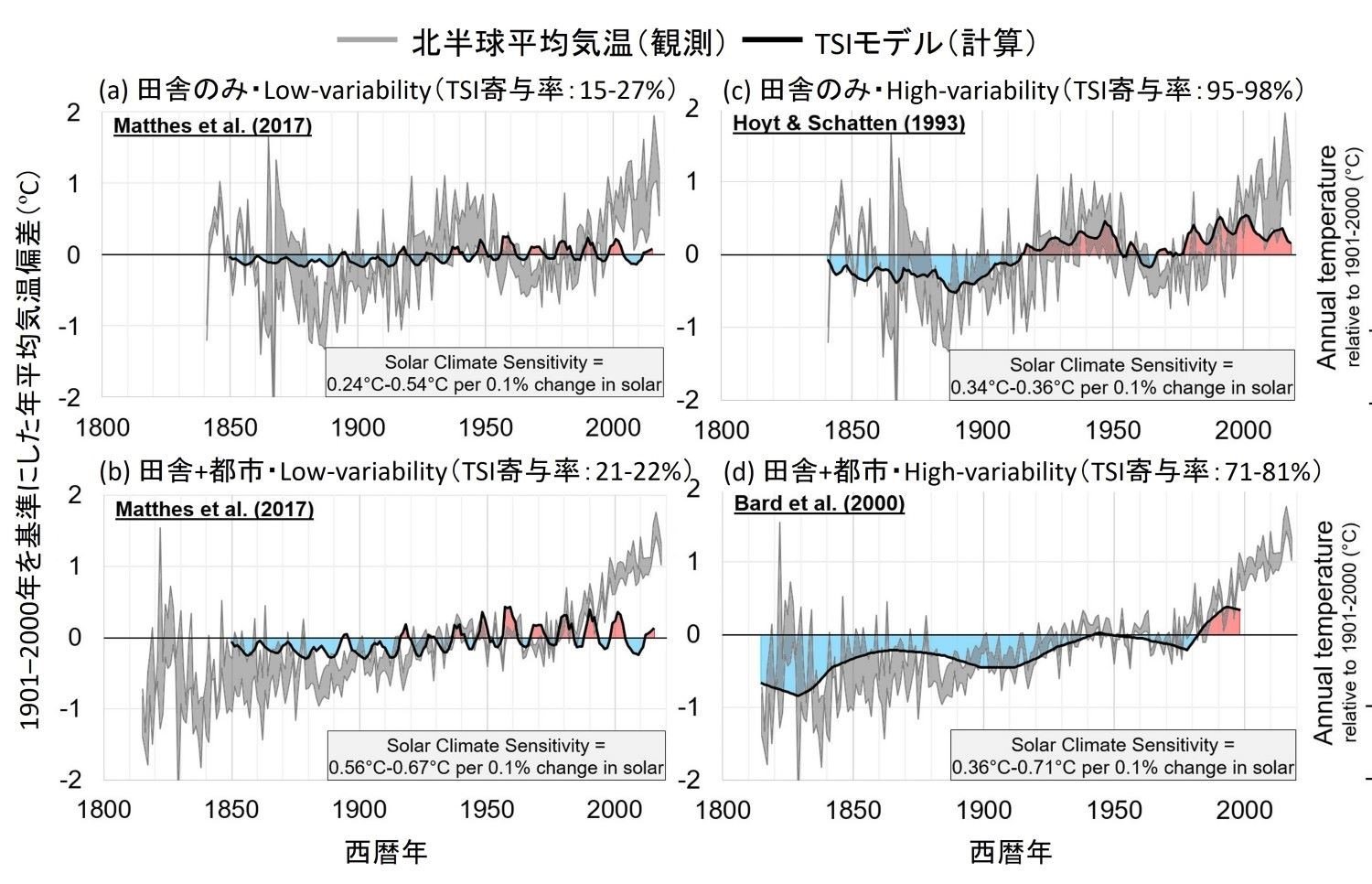
図5(a, c)1800年～2014年における北半球の田舎のみの観測地点および(b, d)全観測地点（田舎・都市両方）の年平均気温の観測結果とLow-variabilityモデル^注16)およびHigh-variabilityモデル^{注15) ，注18)}による太陽総放射量（TSI）の計算結果の時系列変化（Connolly et al., 2021^注1)を著者が和訳）。TSIの計算結果は最小二乗法により気温観測値にフィッティングすることで縦軸のスケールを合わせている。

5．衛星観測データの蓄積のみが論争を終わらせる

過去のTSIが数十年規模で大きく変動したというHigh-variabilityモデルにはこれほどのインパクトがありながら、最新のIPCCではほとんど検討されていない。図2aの引用元である2001年のIPCC報告書^注9)では、過去のTSIの絶対値とその再構築の方法には大きな不確実性を伴うため、科学的理解は非常に低い（level of scientific understanding is very low）とされていた。2007年の報告書^注5)でも、図3のように High-variabilityモデルを含めたさまざまなシナリオが検討されていた。ところが、最新の報告書^注19)では「非常に高い（very high）」という確信度で太陽活動の影響は小さいとして、Low-variabilityモデル（Matthes et al., 2017）^注16)のみを最新の気候モデル相互比較研究CMIP6に採用としている。そして、High-variabilityモデル（Egorova et al., 2018^注20) ）は「静かな太陽（太陽黒点数がゼロのときの太陽）からのTSIの長期データがないため仮説に過ぎない」という理由で却下されている。

著者が調べた限り、衛星観測期間のACRIM gapの謎は今も未解決である。この問題が残っている以上、 TSIによる気温上昇率の見積もりとその結果に依存する地球温暖化量の評価には大きな不確実性が含まれているはずである。この不確実性を減らすためには、現在も蓄積され続けている衛星観測データに基づいて太陽定数が定数なのかどうかを検証し続ける以外にないと思われる。

ところで、本稿で示した結果ではTSIと地球の気温上昇が比例すると仮定されているが、実際にはこれほど単純ではない。太陽と気候の関係は非線形であり、大気と海洋の間の熱の循環パターンを変化させることなどが考えられる^{注21) ，注22)}。TSI以外にも，太陽からの紫外線量、太陽フレアに伴い放出される荷電粒子（太陽宇宙線）、遠方の超新星爆発から飛来する銀河宇宙線量の変動も地球の気温上昇をもたらす可能性があり^注23)、太陽活動と関係している研究課題はまだまだ残っている。

注1）

Connolly, R., Soon, W., Connolly, M., Baliunas, S., Berglund, J., Butler, C.J., Cionco, R.G., Elias, A.G., Fedorov, V.M., Harde, H., Henry, G.W., Hoyt, D.V., Humlum, O., Legates, D.R., Lüning, S., Scafetta, N., Solheim, J.-E., Szarka, L., Loon, H., Herrera, V.M.V., Willson, R.C., Hong Yan, H. and Zhang, W. (2021) How much has the Sun influenced Northern Hemisphere temperature trends? An ongoing debate, Research in Astronomy and Astrophysics, 21, 131.

注2）

CDN (2022) Looking At The Sun（動画）
https://www.youtube.com/watch?v=rJIw7ulYaGk

注3）

Arias, P.A., et al. (2021) Technical Summary. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, UK and New York, NY, USA, 33-144.

注4）

太陽の科学館（2021）黒点～磁場が通り抜ける「穴」～
https://solarphys.com/dynamics/sunspot/

注5）

Forster, P. et al. (2007) Changes in Atmospheric Constituents and in Radiative Forcing, In: Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, UK and New York, NY, USA.
https://www.ipcc.ch/report/ar4/wg1/

注6）

CarbonBrief (2021) 深掘りQ&A: 気候科学に関するIPCCの第6次評価報告書
https://www.carbonbrief.org/in-depth-qa-the-ipccs-sixth-assessment-report-on-climate-science-japanese/

注7）

小倉義光（2016）一般気象学　第2版補訂版，東京大学出版会，320pp．

注8）

WDC-SILSO (Sunspot Index and Long-term Solar Observations)データベース（2023）Total sunspot number, 13-month smoothed monthly total sunspot number [1/1749 – now]
https://sidc.be/silso/datafiles

注9）

Ramaswamy, V., et al. (2001) Observed Climate Variability and Change. In: Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 881pp.
https://www.ipcc.ch/report/ar3/wg1/

注10）

Scafetta, N. and Willson, R.C. (2014) ACRIM total solar irradiance satellite composite validation versus TSI proxy models, Astrophysics and Space Science, 350, 421–442.

注11）

Willson, R.C. and Mordvinov, A.V. (2003) Secular total solar irradiance trend during solar cycles 21–23, Geophysical Research Letters, 30, 1–4.

注12）

Fröhlich, C. and Lean, J. (2004) Solar radiative output and its variability: Evidence and mechanisms, The Astronomy and Astrophysics Review, 12, 273–320.

注13）

Lockwood, M. (2012) Solar influence on global and regional climates, Surveys in Geophysics, 33, 503–534.

注14）

Kopp, G. and Lean, J. (2011) A new, lower value of total solar irradiance: Evidence and climate significance, Geophysical Research Letters, 38, L01706.

注15）

Hoyt, D.V. and Schatten, K.H. (1993) A discussion of plausible solar irradiance variations, 1700–1992, JGR: Space Physic, 98, 18895–18906.

注16）

Matthes, K., Funke, B., Andersson, M.A., Barnard, L., Beer, J., Charbonneau, P., Clilverd, M.A., Dudok de Wit, T., Haberreiter, M., Hendry, A., Jackman, C.H., Kretzschmar, M., Kruschke, T., Kunze, M., Langematz, U., Marsh, D.R., Maycock, A.C., Misios, S., Rodger, C.J., Scaife, A.A., Seppälä, A., Shangguan, M., Sinnhuber, M., Tourpali, K., Usoskin, I., van de Kamp, M., Verronen, P.T. and Versick, S. (2017) Solar forcing for CMIP6 (v3.2), Geoscientific Model Development, 10, 2247–2302.

注17）

堅田元喜 (2022) 20世紀前半の中国の気温も、現在と同じくらい高かった？
https://ieei.or.jp/2022/03/expl220314/

注18）

Bard, E., Raisbeck, G., Yiou, F. and Jouzel, J. (2000) Solar irradiance during the last 1200 years based on cosmogenic nuclides, Tellus, 52, 985–992.

注19）

Forster, P., et al. (2021) The Earth’s Energy Budget, Climate Feedbacks, and Climate Sensitivity. In: Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press. In Press.
https://www.ipcc.ch/report/ar6/wg1/chapter/chapter-7/

注20）

Egorova, T., Schmutz, E., Rozanov, E., Shapiro, A.I., Usoskin, I., Beer, J., Tagirov, R.V. and Peter, T. (2018) Revised historical solar irradiance forcing, Astronomy & Astrophysics, 615, A85.

注21）

Scafetta, N. (2019) On the reliability of computer-based climate models, Italian Journal of Engineering Geology and Environment, 1, 49–70.

注22）

Tanaka, H.L. and Tamura, M. (2016) Relationship between the Arctic oscillation and surface air temperature in multi-decadal time-scale, Polar Science, 10, 199–209.

注23）

宮原ひろ子（2014）地球の変動はどこまで宇宙で解明できるか、化学同人、232pp．