ミクロとマクロの狭間で：経済系における真の集団運動を検出する！

　経済現象に対するミクロの視点とマクロの視点とは本質的に異なる。経済学の教科書は、確かにミクロとマクロに分かれているものの、現在主流の経済学では、ミクロの視点に重きが置かれ、マクロの視点はミクロの視点の単なる延長線上に過ぎない。筆者は、株式市場の振る舞い、景気循環、物価変動などを個々の要素の集団運動として捉え、それらの経済現象について実証的な研究を行ってきた。経済系におけるマクロの集団運動の存在をデータから裏付けることできれば、マクロ経済学の復権が可能となるのである。しかし、実際の経済データはノイズまみれであり、真の集団運動を検出するためには、最新のデータ分析手法を駆使する必要がある。筆者のこのような野望の一端を紹介する。^注1

注1 本稿は、近々出版される次の論文の内容をかみ砕き、解説したものである：
Hiroshi Iyetomi, "Collective Phenomena in Economic Systems", Chap. 9 in Complexity, Heterogeneity, and the Methods of Statistical Physics in Economics, eds. Hideaki Aoyama, Yuji Aruka, and Hiroshi Yoshikawa, Springer Nature Singapore Pte Ltd.

1.　はじめに

　最近、ムクドリが大群で街路樹に住み着き、騒音や衛生上の問題を引き起こしている。筆者の大学キャンパス内でも、初夏の夕方になるとムクドリたちが喧しく鳴いている。ムクドリたちは何かに驚くと、空中で図1のような一体となった群遊行動をとることがしばしば観察される。あたかも、ムクドリたちがリーダーを事前に決め、リーダの命令下で統一的に行動しているかのようである。もちろん、ムクドリたちの間にそのような指揮命令系統は存在しない。ムクドリ個々は、近くの仲間の飛び方を真似るだけの簡単な行動ルールに従っているに過ぎない。そのようなムクドリ間の単純な相互作用が、人にとって不可思議な群遊行動を生んでいる。ムクドリたちは、自分がそのようなマクロの集団運動の構成要素であることは知覚していない。ムクドリの群遊行動のような身近な現象にも、本稿の問題意識が潜んでいる。つまり、ミクロの視点とマクロの視点とは本質的に異なるとのメッセージである。このような問題意識には、ミクロ（要素）とマクロ（全体） を同時に考えられる人間の知性が反映されているのである。

図1　ムクドリたちの群遊行動

（新潟大学五十嵐キャンパスで筆者撮影）

　筆者の専門分野は経済物理学である。物理学の考え方や数理的手法を援用し、複雑な経済現象を読み解くことを試みている。景気循環が経済主体の個別的活動の集積によって生まれるのは言うまでもない。他方で、ムクドリたちの群遊行動の例から明らかなように、個々の活動を追跡しただけでは、経済全体の振る舞いを知ることはできない。ミクロの経済とマクロの経済をどのようにつなぐかが問題である。ミクロとマクロの関係が明らかになれば、経済施策を立案するにあたって大いに役立つであろう。物理学においては統計物理学という学問がミクロとマクロとの架け橋となっている。このような物理学と経済学とのアナロジーを追求するのも経済物理学の醍醐味である。

　経済学の教科書も確かにミクロとマクロに分かれているものの、現在主流の経済学では、ミクロの視点に重きが置かれ、マクロの経済はミクロの経済の単なる相似拡大と見なされている。経済学においては、アダム・スミスの国富論を源流に最小単位の経済主体の行動を扱うためミクロ経済学がまずは構築された。他方、マクロ経済学は、ジョン・メイナード・ケインズという不世出の天才の洞察によって確立された。ミクロ経済学は、我々の身の回りに立脚しているため、その存在意義に疑問がもたれることはない。ところが、マクロ経済学の実証的基盤は脆弱であり、そのミクロ的基礎づけに疑義があるとして、マクロ経済学は現在の閉塞的な状況に陥ってしまっている。

　筆者は、株式市場の振る舞い、景気循環、物価変動などを個々の要素の相互作用に基づく集団運動として捉え、それらの経済現象について実証的な研究を行ってきた。本稿では、最近得られた研究成果のいくつかについて紹介する。経済系におけるマクロの集団運動の存在をデータから裏付けることができれば、マクロ経済学の復権が可能となるとの野望をもっているのである。しかし、実際の経済データはノイズまみれであり、真の集団運動を検出するためには、最新のデータ分析手法を駆使する必要がある。

2.　ランダムの幻想

　景気循環のような周期運動を観測すると、人はその背景に何か明確な要因が隠されていると期待する。もちろん、太陽活動の変動のような外生的要因によって周期性が生じる場合があることは自明である。景気を自律的に循環させる内生的メカニズムもすぐに思い浮かぶ。例えば、家計が豊かであると消費が増え、企業は生産を増やし、景気が上向く。ところが消費が拡大し過ぎると、生産が追いつかず物価が上昇する。そのような状況になると、逆に消費が落ち込み始め、企業も生産を控えるようになり、不景気となる。さらに消費が落ち込むと、物価が下がり、消費が増え、景気が再び良くなるという具合である。

　ところが、そうは問屋が卸さない。1920 年代にユールとスルツキーは必然と偶然とを見分ける難しさを独立に指摘したのである。図2(a) にその例を示す。まず正規分布（平均0、 分散1）に従う乱数を発生させ、時系列の原データ（灰色の細線）とした。さらにそのように得られた時系列に対して10 項移動平均操作を施した（黒い太線）。平滑化されたデータには、循環的変動が内在しているように見える。もちろんこれは偶然の産物である。景気循環を抽出する試みを含めて経済時系列データの解析では、移動平均法がしばしば用いられる。また、月次単位や年単位で計測される原データそのものにも、暗々裏のうちにある種の移動平均操作が紛れ込むであろう。このユール・スルツキー効果が、経済が合理的期待形成に基づく均衡状態にあることを大前提する実物的景気循環(RBC) 理論において景気循環の存在の説明に用いられる。技術進歩などによるランダムな生産性ショックが、経済系に対する確率的な擾乱（かくらん）の役割を果たし、ユール・スルツキー効果によって景気循環を生むという仕掛けである。観測される景気循環は、RBC モデルの枠組みでユール・スルツキー効果によって説明されるランダムの幻影に過ぎないのであろうか。

図2　(a・上) ランダム時系列とその移動平均　(b・下) ランダム時系列の外見周期

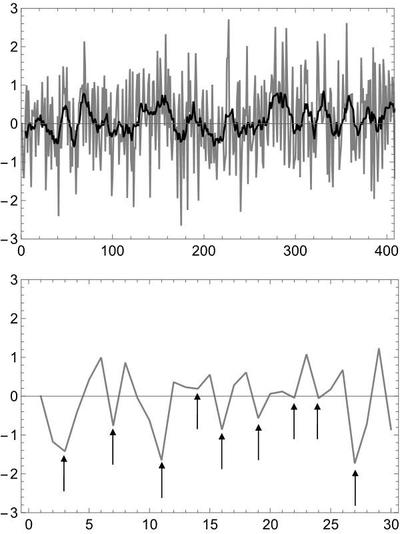※クリックでオリジナル画像表示

　実は、移動平均操作なしの原データにおいてすら外見上の周期性が観測されるのである。図2(b) では、図2(a) の最初の30 点の振る舞いが拡大され、極小の位置が矢印で示されている。極小がほぼ3点毎に現れることがわかる。もちろん、この周期変動もランダムの幻影である。この事実は複雑系科学の父とも言える寺田寅彦によって1916 年に初めて指摘され、現実のデータを解析するにあたって警鐘が鳴らされた。なお、その数十年後に伏見康治によって隣接する極小の間隔の平均が3であることが数理的に示された。寺田の生きた時代、物理学ではミクロ（原子・分子）の世界の基本法則である量子力学が勃興・発展し、すべてを要素に還元する考え方が主流であった。その中で、寺田は日常の現象（破壊や放電のパターン、雪の結晶成長、風紋、人流、金平糖の角、線香花火など枚挙にいとまがない）に着目し、いくつもの先駆的研究を行った。現在では、そのようなマクロの視点は、複雑系科学として大きな学問の潮流をなしている。人の数理的解析能力は限られており、複雑系科学ではコンピューターによるシミュレーションが重要な役割を果たす。寺田は時代を先取りし過ぎてしまった。

3.　実数から複素数へ

　筆者らは、複雑多体系における要素間の動的相関を効果的に検出できる複素ヒルベルト主成分分析(CHPCA) 法を発展させてきた。この数理的手法は、ノイズに隠されたリード・ラグ関係を内包した集団運動の解析にあたって、従来の主成分分析(PCA) 法と比較し、はるかに優れている。図1 のムクドリの群遊行動をもう一度参考にしてみると、集団運動の中でムクドリのあるものは先んじて動き、あるものは遅れて追随していることがわかる。経済系においても、変量同士がいつも同期しているわけではなく、それらの変動に時間差が存在する場合も容易に想像される。

　CHPCA 法は、実の時系列データからそのヒルベルト変換を虚部として複素時系列データを生成することから出発する。ヒルベルト変換は時系列データの位相（偏角とも呼ばれる）を90 度ずらす働きをもつ。実は、ヒルベルト変換を使った実時系列データの複素化は、1 次元方向の正弦振動（単振動）を2 次元の複素平面における等速円運動への拡大操作に対応する。逆に、複素平面内での等速円運動を実軸へ射影すると、正弦振動に回帰する。もし図3(a) で示すようなある一定のリード・ラグ関係にある2 つの正弦振動があれば、それらは図3(b) で示すように一定の位相差をもった2 つの等速円運動へ拡大される。回転運動は時計回り、反時計回りのどちらも可能であり、本稿では時計回りを採用する。つまり、位相が小さい時系列ほど先行する。このようなデータ表現の工夫によって、2 つの正弦振動のリード・ラグ関係を位相差として容易に読み取ることができるようになる。なお、円運動の半径が振動の振幅に対応することにも注意する。

図3　(a) 2つの正弦振動　(b) それらの複素数表

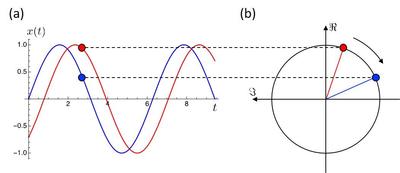※クリックでオリジナル画像表示

　CHPCA の次のステップでは、複素時系列の各ペアについて相関係数を計算する。このように計算された相関係数は一般に複素数であり、その絶対値が時系列間の相関強度、位相が時系列間のリード・ラグ関係を表す。特に、実時系列データから計算される通常の相関係数では無相関と判定されるsin 波とcos 波の時系列ペアであっても、複素化された時系列データを用いて相関係数を計算すれば、実部と虚部とのクロス項からそれらのラグ相関を検出できる。得られた複素相関係数を成分にもつ行列に対する固有値問題を解くことにより、多体系における主成分（固有振動モード）を特定できる。なお、CHPCA で対象が実数から複素数へ拡大されても計算の煩雑度は増大しない。

　主成分の重要度を表す複素相関行列の固有値を大きいものから下降順に並べたとき、どこまでの固有値が統計的に有意味であるかの判定は、CHPCA に限らず元のPCA からの重要な方法論的課題である。筆者らは、ノイズに埋もれた真の相関情報を抽出するにあたって、ランダム行列理論(RMT) と呼ばれる数学を用いた。時系列データの複素化に呼応して、統計ノイズを除去するための帰無仮説となるRMT の固有値分布式を変更する必要であるが、もし相関行列がRMT によって予測される最大固有値より大きい固有値を持てば、それは真の相関の現れと判断できる。

4.　株式市場の動き

　まず株式市場の集団的振る舞いに目を向けてみる。ここで紹介する株式市場に関する結果は、S&P 500 の24 業種483 銘柄に対する1009 営業日(2008 年1 月2 日から2011 年12 月30 日まで) の株価日次データに基づいている。 図4は、20 の銘柄をランダムに選び出し、それらの株価の日次変動（対数リターン）を比較している。リーマンショック時にはボラティリティーの協調的増加が一時的に観測されるが、「心眼」をもっていればいざ知らず、株価同士の間にある何らかの連関性を目で読み取ることは困難であろう。この点は、冒頭で触れた目視で明らかなムクドリの群遊行動と大きく異なり、最新の数理的解析手法が必要とされる所以である。

図4　S&P 500 の個別銘柄20 種の対数リターン

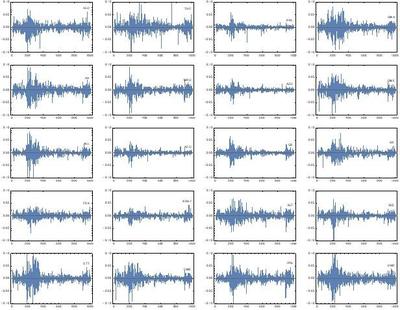※クリックでオリジナル画像表示

図5　(a) S&P 500 の市場モード　(b) 市場モードにおける業種間のリード・ラグ関係

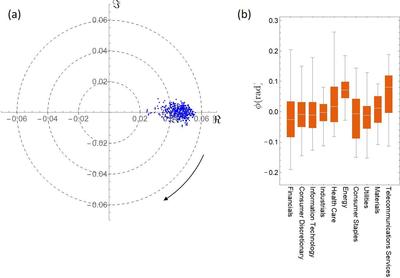※クリックでオリジナル画像表示

　図5(a) に、複素相関行列の最大固有値に対応する固有ベクトルの各成分を複素平面上で表示した。図3の例を思い起こしていただきたくと、この固有ベクトルは、すべての株価がほぼ一団となって変動する様子（市場モードと呼ばれる）を表していることがわかる。市場全体の動きを表すために、代表的銘柄の株価を集約するよって様々な株式インデックスが考案されている。市場モードの存在は、そのような株式インデックスを意味づける。固有ベクトルをより詳しく見れば、銘柄間にリード・ラグ関係が存在することがわかる。図5(b) は、10大業種ごとに株価の位相の分布を箱ひげ図で表示したものである。金融業、生活必需品業の株価が先行するのに対して、エネルギー業、情報通信業、医療産業の株価が遅行することがわかる。このような銘柄間のリード・ラグ関係を取り入れた新しい株式インデックスの構築が期待される。

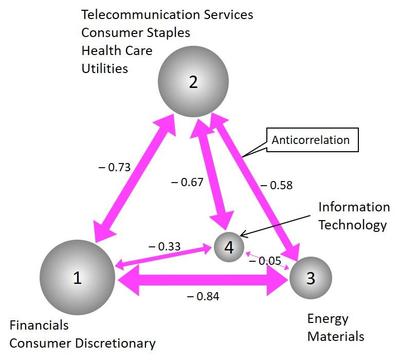
　さらに、市場モードを取り除いた後に残る株価間の相関（多粒子系における重心から観測した各粒子の運動間の相関に対応）に着目すると、株価は同期的に変動する4つのグループを構築する。図6で示すように、それらのグループは業種で特徴づけられ、互いに反相関関係にある。中でも、情報産業グループを除く3つのグループは互いに強い競合関係にあり、3すくみの状況（敵の敵は敵！）である。静的に安定な状態を導かない市場に潜むこのような相関構造が、株式市場の複雑な振る舞いを生む要因となっている可能性がある。

図6 S&P 500 におけるグループ相関構造

※クリックでオリジナル画像表示

5.　景気循環

　景気の現状を把握し、将来予測を行うための指標として景気動向指数があり、毎月内閣府から公表されている。生産、雇用など様々な経済活動を表すマクロ経済指標の動きの集約である景気動向指数は、景気を経済活動の総体として定義しているとも言える。景気動向指数には、景気に対し先行して動く先行指数、ほぼ一致して動く一致指数、遅れて動く遅行指数の3 本の指数がある。 景気の現状把握には一致指数が利用される。一致指数に対して数ヶ月先行すると推定されている先行指数は、景気の動きを予測する目的で使われる。 遅行指数は、一般的に一致指数に対して数ヶ月から半年程度遅れて追随し、事後的な確認に用いられる。これらの指数は基礎指標（2016 年1 月時点で先行指数11、一致指数10、遅行指数9 の計30 系列）から計算されている。本研究では2000 年1 月から2014 年12 月まで計180 ヵ月の期間に着目する。解析を始めるにあたっては、各時系列の対数差分（正負の値をとる量については差分）をとることにより、データを定常化する。株価の場合と同じく、基礎指標の先行性、一致性、遅行性を目視で見極めることは難しい。景気動向指数は経済学者の叡智の結晶と言っても過言ではない。

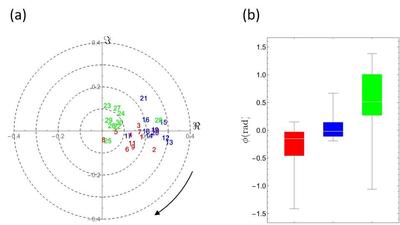
図7　(a) 景気動向基礎指標群の集団運動（赤は先行、青は一致、緑は遅行指標を表す）
　　　 (b) 先行、一致、遅行の各基礎指標群における位相分布

※クリックでオリジナル画像表示

　図7(a) は、CHPCA で得られた最大固有値に対応する固有ベクトルである。株式市場における市場モードに類似して、景気動向基礎指標の集団運動を表している。図7(b) は、3グループにおける位相分布を箱ひげ図表示したものである。これらの図から基礎指標30 種類のリード・ラグ関係を読み取ると、概ねそれらの先行性、一致性、遅行性が再現されることがわかる。しかし、いくつかの基礎指標については、内閣府によるアサイメントとは異なるリード・ラグ特性をもっている。例えば、指標28 の「きまって支給する給与（製造業、名目）」は遅行指標と分類されているが、CHPCA に依れば、むしろ他の一致基礎指標と同じように動くと期待される。逆に、指標21「有効求人倍率( 除学卒)」は、むしろ遅行基礎指標とみなすべきとの解析結果である。

　以上のように、本研究は、あらためて人の知力の凄さを確認したともに、数理的アルゴリズムを使って多数の経済基礎指標のプールから適切な指標を機械的に選択し、代表的マクロ経済変数を構築する道を切り開く。

6.　物価変動

　インフレ/ デフレとは、個別物価の平均で算出された物価水準の上昇/ 下降として定義される。従来の経済学では、個別物価同士は独立に振る舞い、共通の外的ショックによって物価水準が上下すると考えられてきた。しかし、現実には企業同士は取引関係などによって強く結びつき、企業間相互作用が個別物価の集団運動の可能性など物価のダイナミクスにも重要な影響を与えていると推察される。個別物価の集団運動としてインフレ/ デフレを実証的にもう一度見直してみる。

　最近では、消費者物価指数などの公的統計データばかりではなく、オルタナティブ・データと呼ばれる新しい民間のデータが注目されている。我が国では、いち早くスーパーマーケットのPOS(Point of Sale) データに基づく日経・東大日次物価指数 ( 現名称はCPINow) の公開が2014 年から開始された。消費者物価の動向をほぼリアルタイムで日次計測するという試みである。日本全国約300 店舗で販売される20 万点以上の商品について収集された日々の価格および販売数量が原データとなっている。他方、ある月の消費者物価指数はサンプル調査に基づき、しかも翌月の月末に公表されるため、網羅性・迅速性を欠いている。では、消費者物価指数と日経・東大日次物価指数との関係はどのようであろうか。

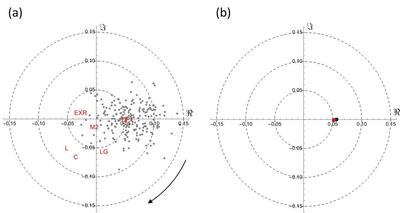
図8　(a) POS 価格（灰色の点）の集団運動とマクロ経済変数　(b) POS 価格群の重心（黒い点）と消費者物価指数（赤い点）

※クリックでオリジナル画像表示
（L: 先行指数、C: 一致指数、LG: 遅行指数、M2: マネーストック、EXR: 円ドル為替レート、CPI: 消費者物価指数）

　月次であるものの、品目別のPOS 価格データもホームページ上(https://www.cmdlab.co.jp/price_u-tokyo/monthly-item-tm/) で公開されている。図8(a) では、最大固有値に対応する固有ベクトルの各成分が複素平面上で表示されている。POS 価格ばかりではなく、消費者物価指数、景気動向指数（先行、一致、遅行）、マネーストック、円ドル為替レートも付け加えられている。同図からPOS 価格の集団運動の存在を明確に確認できる。しかも景気がPOS 価格の集団運動および消費者物価を先導していることがわかる。（先に触れたように、一致指数と遅行指数との時間間隔は数ヶ月から半年程度であるので、物価は1 年以上のラグをもって景気に追随） つまり、景気が上向くと、物価の集団運動としてのインフレが追随する。それに比し、金融変数の集団的な物価変動に対する影響は小さい。POS 価格の重心を計算してみると、図8(b) で示すように、消費者物価と極めてよく一致し、物価の集団運動を考える限り、両者は同じ情報を表していると言ってよい。なお、POS 価格の集団運動の強度は全体の価格変動の約7.3% に過ぎない。そのためノイズが相対的にとても大きく、目視でPOS 価格の集団運動を検出することは不可能である。

7.　おわりに

　筆者は、ある国際会議に出席するため、昨年の夏にギリシャのスペッツェス島を訪れる機会があった。スペッツェス島は、アテネ近くのピレウスから高速艇を使って2時間余りのところに位置する風光明媚な小島である（図9）。著名な観光ルートから外れているせいか観光客は思いの外少なく、豊かな自然を大いに満喫することができた。同島は村上春樹氏が3年の海外生活を送った最初の滞在地である。その様子は、「遠い太鼓」として出版されている旅行記から伺い知ることができる。その事実を旅行前に知った筆者は、にわか村上ファンとして、さっそく同書を読んだ。実は、筆者は本をあとがきから読む癖がある。いつもどおりに、あとがきから読み始めた。そこに書かれていたある一節を見つけ、我が意を得たりと思わずほくそ笑んだのである。その一節を引用することによって本稿の終いとする。

『外国に行くとたしかに「世界は広いんだ」という思いをあらたにします。でもそれと同時に「文京区だって（焼津市だって、旭川市だって）広いんだ」という視点もちゃんとあるわけです。僕はこのどちらも視点としては正しいと思います。そしてこのようなミクロとマクロの視点が一人の人間の中に同時に存在してこそ、より正確でより豊かな世界観を抱くことが可能になるはずだと思うのです。僕が三年かけてこの本を書いたことによってなんとなく体得したものがあるとすれば、それはそのような複合的な目であるような気がします。』　　 （村上春樹著「遠い太鼓」（講談社文庫）の 「 文庫本のためのあとがき」から引用）

図9　スペッツェス島（ギリシャ）にて

※クリックでオリジナル画像表示

追記：

　現在の新型コロナウイルス禍では、まさに人の知性が試されています。ミクロとマクロの視点を併せ持ち、この難局を乗り切りましょう。